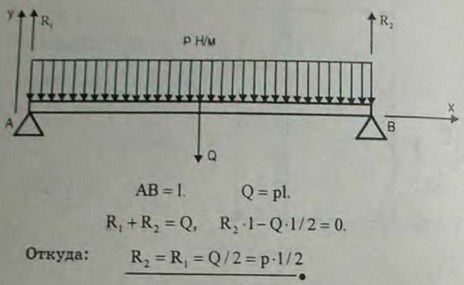
3.1 (3.1). Определить вертикальные реакции опор, на которые свободно оперта у своих концов горизонтальная балка длины l, нагруженная равномерно по р Н на единицу длины. Вес балки считать включенным в равномерно распределенную нагрузку.
Ответ: R1 = R2 = 1/2pl Н.
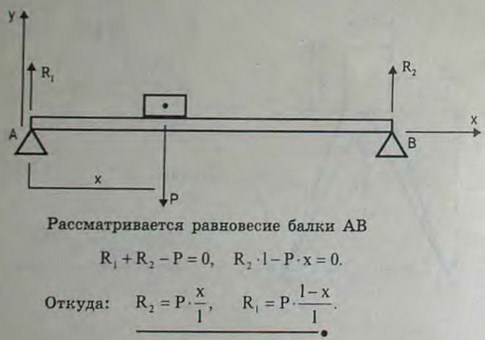
3.2(3.2). Определить вертикальные реакции опор горизонтальной балки пролета l, если груз Р помещен на ней на расстоянии х от первой опоры.
Ответ: R1= P(l-x)/l, R2 = Px/l.
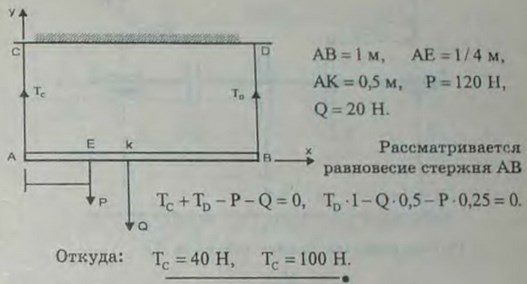
3.3(3.3). Однородный стержень АВ, длина которого 1 м, а вес 20 Н, подвешен горизонтально на двух параллельных веревках АС и BD. К стержню в точке Е на расстоянии АЕ = 1/4 м подвешен груз Р = 120 Н. Определить натяжения веревок ТC и TD.
Ответ: ТC = 100 Н, TD = 40 Н.
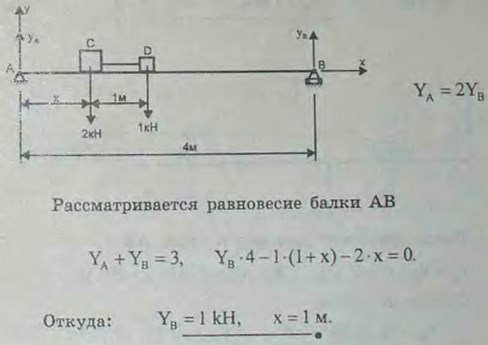
3.4(3.4). На горизонтальную балку, лежащую на двух опорах, расстояние между которыми равно 4 м, положены два груза, один С в 2 кН, другой D в 1 кН, так, что реакция опоры А в два раза больше реакции опоры В, если пренебречь весом балки. Расстояние CD между грузами равно 1 м. Каково расстояние х груза С от опоры A?
Ответ: х = 1 м.
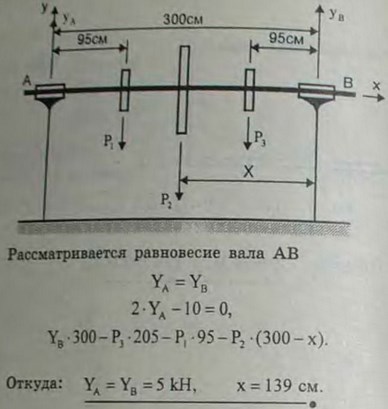
3.5(3.5). Трансмиссионный вал АВ несет три шкива веса Р1 = 3 кН, Р2 = 5 кН, Р3 = 2 кН. Размеры указаны на рисунке. Определить, на каком расстоянии х от подшипника В надо установить шкив веса Р2, чтобы реакция подшипника А равнялась реакции подшипника В; весом вала пренебречь.
Ответ: х= 139 см.
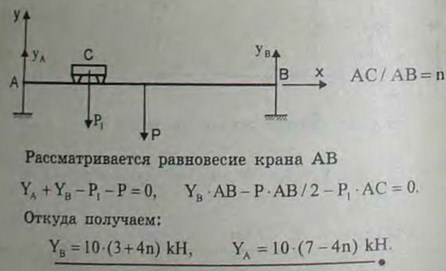
З.6(З.6). Определить силы давления мостового крана АВ на рельсы в зависимости от положения тележки С, на которой укреплена лебедка. Положение тележки определить расстоянием ее середины от левого рельса в долях общей длины моста. Вес моста Р = 60 кН, вес тележки с поднимаемым грузом P1 = 40 кН.
Ответ: FA = (7 - 4n) 10 кН, FB = (3 + 4n) 10 кН, где n = АС/АВ.
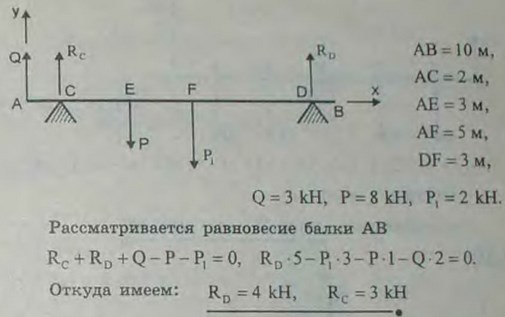
3.7(3.7). Балка АВ длины 10 м и веса 2 кН лежит на двух опорах С и D. Опора С отстоит от конца А на 2 м, опора D от конца В — на 3 м. Конец балки А оттягивается вертикально вверх посредством перекинутого через блок троса, на котором подвешен груз Q веса 3 кН. На расстоянии 3 м от конца А к балке подвешен груз Р веса 8 кН. Определить реакции опор, пренебрегая трением на блоке.
Ответ: RC = 3 кН, RD = 4 кН.
3.8(3.8). Горизонтальный стержень АВ веса 100 Н может вращаться вокруг неподвижной оси шарнира А. Конец В оттягивается кверху посредством перекинутой через блок нити, на которой подвешена гиря веса Р= 150 Н. В точке, находящейся на расстоянии 20 см от конца В, подвешен груз Q веса 500 Н. Как велика длина х стержня АВ, если он находится в равновесии?
Ответ: х = 25 см.

3.9(3.9). Конец А горизонтального стержня АВ веса 20 Н и длины 5 м оттягивается кверху посредством перекинутой через блок веревки, на которой подвешен груз веса 10 Н. Конец В таким же образом оттягивается кверху посредством груза веса 20 Н. В точках С, D, E и F, отстоящих одна от другой и от точек А и В на 1 м, подвешены грузы веса соответственно 5, 10, 15 и 20 Н. В каком месте надо подпереть стержень, чтобы он оставался в равновесии?
Ответ: В середине.

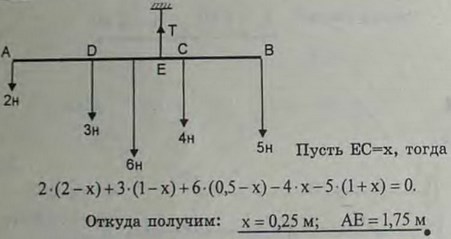
3.10(3.10). К однородному стержню, длина которого 3 м, а вес 6 Н, подвешены 4 груза на равных расстояниях друг от друга, причем два крайних - на концах стержня. Первый груз слева весит 2 Н, каждый последующий тяжелее предыдущего на 1 Н. На каком расстоянии х от левого конца нужно подвесить стержень, чтобы он оставался горизонтальным?
Ответ: х = 1,75 м.
3.11(3.11). Однородная горизонтальная балка соединена со стеной шарниром и подперта в точке, лежащей на расстоянии 160 см от стены. Длина балки 400 см, ее вес 320 Н. На расстояниях 120 см и 180 см от стены на балке лежат два груза веса 160 Н и 240 Н. Определить опорные реакции.
Ответ: 790 Н — вверх, 70 Н — вниз.

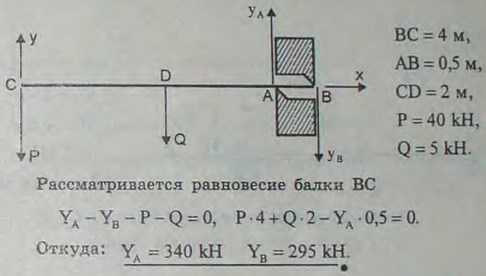
3.12(3.12). Однородная горизонтальная балка длины 4 м и веса 5 кН заложена в стену, толщина которой равна 0,5 м, так, что опирается на нее в точках А и В. Определить реакции в этих точках, если к свободному концу балки подвешен груз Р веса 40 кН.
Ответ: RA = 340 кН — вверх, RB = 295 кН — вниз.
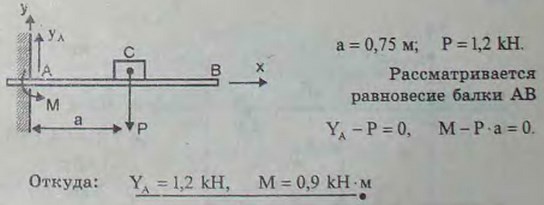
3.13(3.13). Горизонтальная балка заделана одним концом в стену, а на другом конце поддерживает подшипник вала. От веса вала, шкивов и подшипника балка испытывает вертикальную нагрузку Q, равную 1,2 кН. Пренебрегая весом балки и считая, что нагрузка Q действует на расстоянии а = 0,75 м от стены, определить реакции заделки.
Ответ: Реакция R = 1,2 кН, реактивный момент М = 0,9 кН*м.
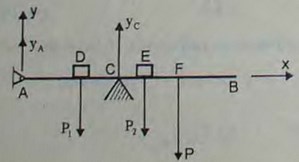
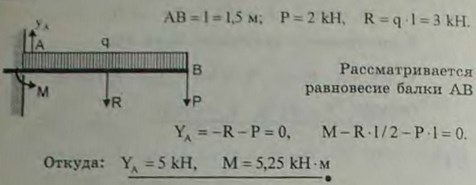
3.14(3.14). Горизонтальная балка, поддерживающая балкон, подвергается действию равномерно распределенной нагрузки интенсивности q = 2 кН/м. На балку у свободного конца передается нагрузка от колонны Р = 2 кН. Расстояние оси колонны от стены l = 1,5 м. Определить реакции заделки.
Ответ: R = 5 кН, М = 5,25 кН • м.
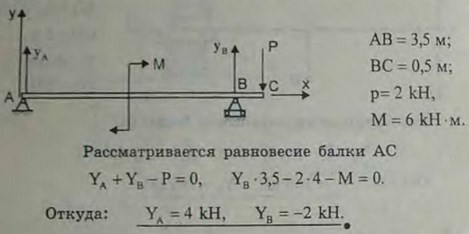
3.15(3.15). На консольную горизонтальную балку действует пара сил с моментом М = 6 кН*м, а в точке С вертикальная нагрузка Р = 2 кН. Длина пролета балки АВ = 3,5 м, вынос консоли ВС = 0,5 м. Определить реакции опор.
Ответ: RA= 2 кН — вниз, RB = 4 кН — вверх.
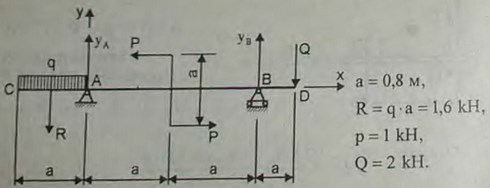
3.16(3.16). На двухконсольную горизонтальную балку действует пара сил (Р, P), на левую консоль — равномерно распределенная нагрузка интенсивности q, а в точке D правой консоли — вертикальная нагрузка Q. Определить реакции опор, если Р = 1 кН, Q = 2 кН, q = 2 кН/м, а = 0,8 м.
Ответ: RA= 1,5 кН, RB = 2,1 кН.
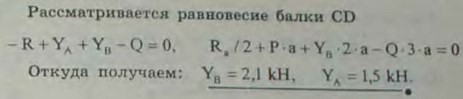
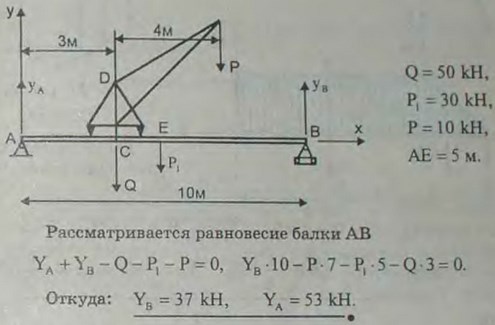
3.17(3.17). На балке АВ длины 10 м уложен путь для подъемного крана. Вес крана равен 50 кН, и центр тяжести его находится на оси CD; вес груза Р равен 10 кН; вес балки АВ равен 30 кН; вылет крана KL = 4 м; расстояние АС = 3 м. Найти опорные реакции в точках А и В для такого положения крана, когда стрелка крана DL находится в одной вертикальной плоскости с балкой АВ.
Ответ: RA = 53 кН, RB = 37 кН.
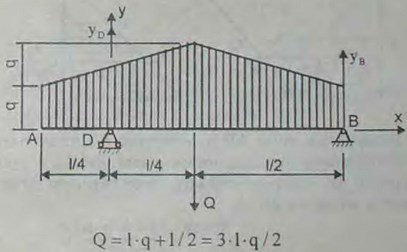
3.18(3.18). Балка АВ длины l м несет распределенную нагрузку, показанную на рисунке. Интенсивность нагрузки равна q Н/м на концах А и В балки и 2q Н/м в середине балки. Пренебрегая весом балки, найти реакции опор D и В.
Ответ: Rd = ql Н, RB = 0,5ql Н.
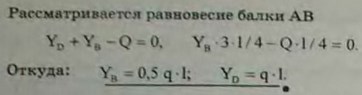
3.19(3.19). Горизонтальная балка АС, опертая в точках В и С, несет между опорами В и С равномерно распределенную нагрузку интенсивности q Н/м; на участке АВ интенсивность нагрузки уменьшается по линейному закону до нуля. Найти реакции опор В и С, пренебрегая весом балки.
Ответ: RB = q/6(3a+3b+a2/b) Н; RC = q/6 (3b-a2/b) Н.
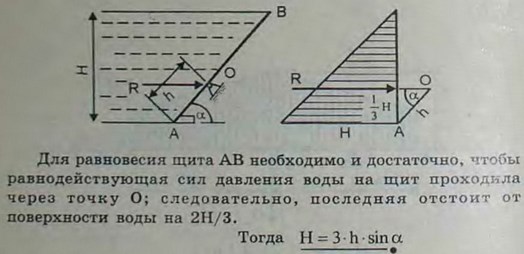
3.20(3.20). Прямоугольный щит АВ ирригационного канала может вращаться относительно оси О. Если уровень воды невысок, щит закрыт, но, когда вода достигает некоторого уровня H, щит поворачивается вокруг оси и открывает канал. Пренебрегая трением и весом щита, определить высоту H, при которой открывается щит.
Ответ: H = Зh sin α.