1.134. Относительно горизонтально расположенного диска, вращающегося с угловой скоростью ω₀, тело, лежащее на диске, находится в покое. Масса тела равна m, расстояние от оси вращения r. а) Какие силы действуют на тело в неподвижной системе отсчета? б) В какой системе отсчета к предыдущим силам добавится только центробежная сила инерции? в) В какой системе отсчета появится еще и сила Кориолиса?

1.135. Какую мощность P развивает сила Кориолиса?

1.136. Какую работу А совершает над частицей кориолисова сила при перемещении частицы относительно вращающейся системы отсчета из точки 1 в точку 2?

1.137. Движение частицы массы m=10,0 г рассматривается в системе отсчета, вращающейся относительно инерциальной системы с угловой скоростью ω=10,0 рад/с. Какую работу А совершают, над частицей силы инерции при перемещении ее из точки, отстоящей от оси вращения на расстояние R₁=1,00 м, в точку, отстоящую на расстояние R₂=2,00 м.

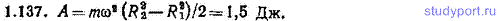
1.138. Небольшое тело падает без начальной скорости на Землю на экваторе с высоты h=10,0 м. В какую сторону и на какое расстояние х отклонится тело от вертикали за время падения τ? Сопротивлением воздуха пренебречь. Сравнить найденное значение х с разностью Δs путей, которые пройдут вследствие вращения Земли за время τ точка, находящаяся на высоте h, и точка, находящаяся на земной поверхности.

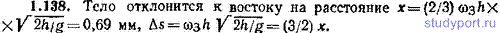
1.139. Имеется горизонтально расположенное ружье, дуло которого совпадает с осью вертикального цилиндра (рис. 1.25). Цилиндр вращается с угловой скоростью ω. а) Считая, что пуля, выпущенная из ружья, летит горизонтально с постоянной скоростью v, найти смещение s точки В цилиндра, в которую попадет пуля, относительно точки А, которая находится против дула в момент выстрела. Решить задачу двумя способами: в неподвижной системе отсчета и в системе отсчета, связанной с цилиндром. б) Зависит ли результат от того, вращается ружье вместе с цилиндром или неподвижно?

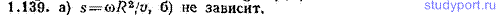
1.140. На широте φ=45° из ружья, закрепленного горизонтально в плоскости меридиана, произведен выстрел по мишени, установленной на расстоянии l=100,0 м от дула ружья. Центр мишени находится на оси ружейного ствола. Считая, что пуля летит горизонтально с постоянной скоростью v=500 м/с, определить, на какое расстояние и в какую сторону отклонится пуля от центра мишени, если выстрел произведен в направлении: а) на север, б) на юг.

1.141. Электровоз массы m=184*10³ кг движется вдоль меридиана со скоростью v=20,0 м/с (72 км/ч) на широте φ=45°. Определить горизонтальную составляющую F силы, с которой электровоз давит на рельсы.

1.142. Горизонтально расположенный диск вращается вокруг оси, проходящей через его центр, с угловой скоростью ω. По диску движется равномерно на неизменном расстоянии от оси вращения частица. Найти мгновенное значение: а) скорости частицы v' относительно диска, при которой сила Кориолиса будет уравновешиваться центробежной силой инерции. Выразить v' через мгновенное значение радиус-вектора r, проведенного к частице из центра диска, б) скорости частицы v относительно неподвижной системы отсчета при тех же условиях.

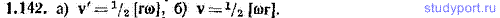
1.143. Горизонтально расположенный стержень вращается вокруг вертикальной оси, проходящей через его конец, с угловой скоростью ω=1,00 рад/с. Расстояние от оси до другого конца стержня l=1,00 м. На стержень надета муфта массы m=0,100 кг. Муфта закреплена с помощью нити на расстоянии l₀=0,100 м от оси вращения. В момент l=0 нить пережигают и муфта начинает скользить по стержню практически без трения. Найти: а) время τ, спустя которое муфта слетит со стержня, б) силу F, с которой стержень действует на муфту в момент τ, в) работу А, которая совершается над муфтой за время τ в неподвижной системе отсчета.

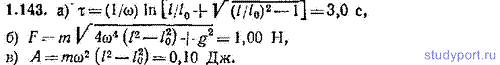
1.144. Горизонтально расположенный диск вращается с угловой скоростью ω. Вдоль радиуса диска движется частица массы m, расстояние которой от центра диска изменяется со временем по закону r = at (a - константа). Найти результирующий момент N сил, действующих на частицу в системе отсчета, связанной с диском. Имеется в виду момент относительно центра диска.

1.145. Имеется система отсчета, вращающаяся относительно инерциальной системы вокруг оси z с постоянной угловой скоростью ω. Из точки O, находящейся на оси z, вылетает в перпендикулярном к оси направлении частица массы m и летит относительно инерциальной системы прямолинейно с постоянной скоростью v. Найти наблюдаемый во вращающейся системе момент импульса M(t) частицы относительно точки O. Показать, что возникновение M(t) обусловлено действием силы Кориолиса.