Еще древние греки обнаружили, что не всегда длину точно заданного отрезка можно выразить с помощью рационального числа. Например, если задан квадрат, длины сторон которого имеют длину, заданную рациональным числом, то какова длина его диагонали? Диагональ можно нарисовать точно, но невозможно выразить ее длину с помощью рационального числа. Такие отрезки называли несоизмеримыми. Однако, греками была разработана теория отношения отрезков, учитывая, что они могут быть несоизмеримы.

Современная математика использует в этом случае понятие иррационального числа.

Иррациональное число – число, которое не может быть представлено ни в виде дроби с целым числителем и знаменателем, ни в виде бесконечной периодичной десятичной дроби. Иррациональные числа могут быть представлены только бесконечными непериодическими дробями.



Примеры иррациональных чисел:

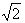- это иррациональное число. 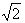= 1, 41…

е = 2,718281828459045…



Действительное числа, вещественное число – это любое рациональное или иррациональное число.

Примеры действительных чисел: 3/5; 1,8; 7,121212…; ….
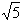