По теореме Ферма достаточное условие экстремума f'(x₀)=0. Значит, для того чтобы найти точки «подозрительные» на экстремум, нужно взять производную от функции f(x₀), приравнять ее к нулю и решить получившееся уравнение. Однако, не все корни этого уравнения будут экстремумами. Для того чтобы выяснить наверняка, является ли точка точкой экстремума, нужно знать достаточное условие экстремума.

Корни уравнения f'(x₀)=0 называют стационарными точками.



Достаточное условие экстремума: Если при переходе через стационарную точку производная меняет знак, то эта точка является экстремумом. Если меняет знак с «+» на «-», то это точка максимума. Если меняет знак с «-» на «+», то это точка минимума.



Если при переходе через стационарную точку производная не меняет знак, то эта точка не является экстремумом.

Очевидно, что точки, в которых функция принимает максимальное значение на некотором промежутке нужно искать среди точек максимума. А точки, в которых функция принимает минимальное значение - среди точек минимума. Однако нельзя забывать, что максимальное (минимальное) значение функция может принимать и на концах промежутка.



Для нахождения максимального или минимального значения функции применяют следующий алгоритм:

1. Берем производную от функции.

2. Находим стационарные точки, решая уравнение f'(x₀)=0.

3. Проверяем достаточное условие экстремума. Выбираем те точки, в которых это условие выполняется.

4. Вычисляем значения функции в найденных точках и на концах промежутка. Самое маленькое значение будет минимальным значением функции на этом промежутке. А самое большое – максимальным.



Пример: Найти максимальное и минимальное значение функции  на промежутке

1. .

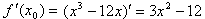2. 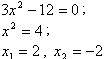. -2 не входит в заданный промежуток.

3. При 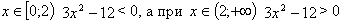. То есть, достаточное условие экстремума выполняется.

4. Вычислим значения функции в точке экстремума и на концах промежутка:



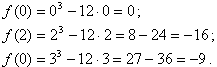
Ответ: функция принимает минимальное значение на промежутке [0;3], при x=2, f(2)=-16,

функция принимает максимальное значение на промежутке [0;3], при x=0, f(0)=0.